Binary Tree Traversals Often we wish to process a binary tree by 'visiting' each of its nodes, each time performing a specific action such as printing the contents of the node. Any process for visiting all of the nodes in some order is called a. Any traversal that lists every node in the tree exactly once is called an of the tree's nodes. Some applications do not require that the nodes be visited in any particular order as long as each node is visited precisely once. For other applications, nodes must be visited in an order that preserves some relationship. Implementation Now we will discuss some implementations for the traversals, but we need to define a node ADT to work with. Just as a linked list is composed of a collection of link objects, a tree is composed of a collection of node objects.

Here is an ADT for binary tree nodes, called BinNode. This class will be used by some of the binary tree structures presented later. Member functions are provided that set or return the element value, return a pointer to the left child, return a pointer to the right child, or indicate whether the node is a leaf.

Download the latest version of Huawei Mobile Connect 3G Modem drivers. MI_00 - USB VID. Pro and Vista. - If you are looking drivers + application. Unlock Huawei & ZTE Modem Free. Unlock Modem; Download Latest Huawei Modem Drivers 64 bit and 32 bit for all latest. Hi there, I have a usb dongle huawei. Download the latest drivers for your Huawei USB MODEM Device to keep your Computer up-to-date. Huawei usb modem. 51 rows Download the latest drivers for your Huawei Modems to keep your.

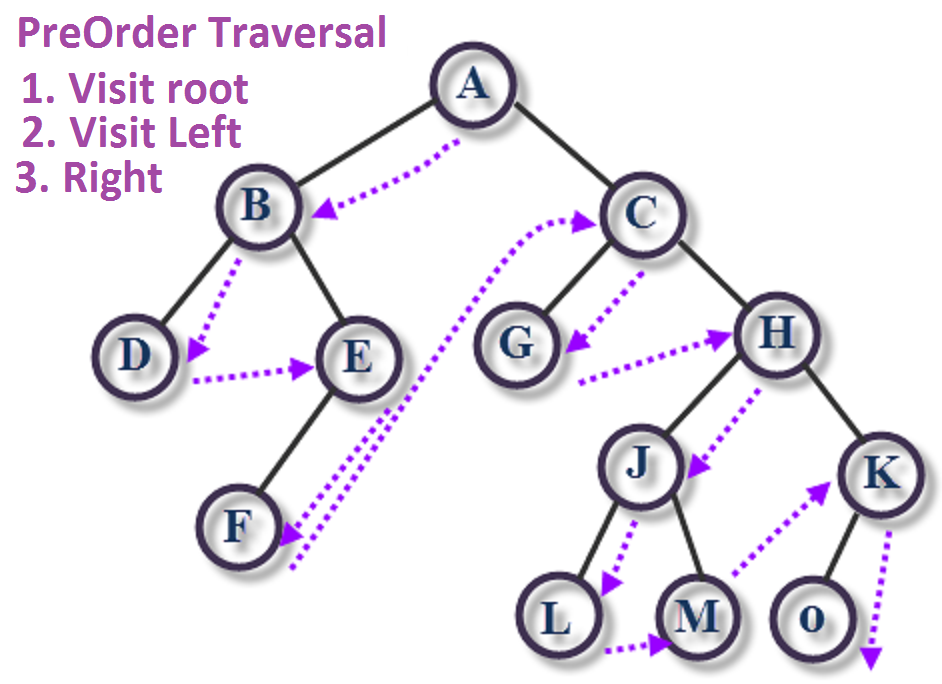
Since the algorithm completely determines the order in which nodes are visited, there is only one possible left-to-right pre-order traversal for each binary tree. Traversing Trees • preorder traversal Algorithm preOrder(v) “visit” nodev for each child w of v do. Traversing Trees • inorder traversal of a binary tree.

Traversal is a process to visit all the nodes of a tree and may print their values too. Because, all nodes are connected via edges (links) we always start from the root (head) node. That is, we cannot randomly access a node in a tree.

There are three ways which we use to traverse a tree − • In-order Traversal • Pre-order Traversal • Post-order Traversal Generally, we traverse a tree to search or locate a given item or key in the tree or to print all the values it contains. In-order Traversal In this traversal method, the left subtree is visited first, then the root and later the right sub-tree. We should always remember that every node may represent a subtree itself.

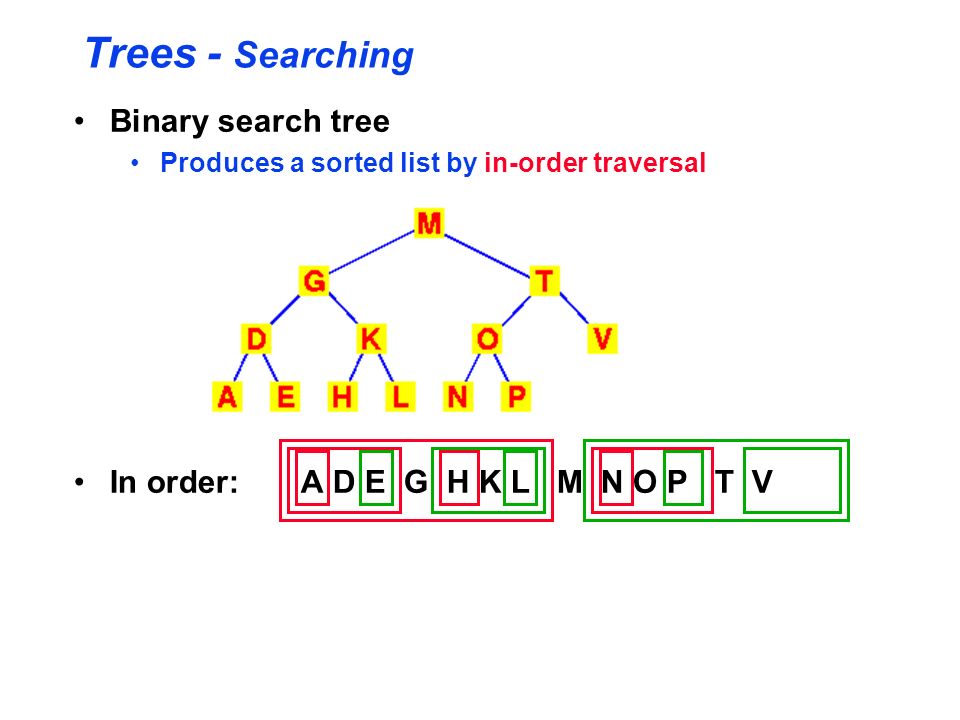
If a binary tree is traversed in-order, the output will produce sorted key values in an ascending order. We start from A, and following in-order traversal, we move to its left subtree B.

B is also traversed in-order. The process goes on until all the nodes are visited. The output of inorder traversal of this tree will be − D → B → E → A → F → C → G Algorithm Until all nodes are traversed − Step 1 − Recursively traverse left subtree.

Step 2 − Visit root node. Step 3 − Recursively traverse right subtree.

Pre-order Traversal In this traversal method, the root node is visited first, then the left subtree and finally the right subtree. We start from A, and following pre-order traversal, we first visit A itself and then move to its left subtree B. B is also traversed pre-order. The process goes on until all the nodes are visited. The output of pre-order traversal of this tree will be − A → B → D → E → C → F → G Algorithm Until all nodes are traversed − Step 1 − Visit root node. Step 2 − Recursively traverse left subtree. Step 3 − Recursively traverse right subtree.

Post-order Traversal In this traversal method, the root node is visited last, hence the name. Pdf mystery method the venusian arts handbook pdf. First we traverse the left subtree, then the right subtree and finally the root node. We start from A, and following Post-order traversal, we first visit the left subtree B. B is also traversed post-order.

The process goes on until all the nodes are visited. The output of post-order traversal of this tree will be − D → E → B → F → G → C → A Algorithm Until all nodes are traversed − Step 1 − Recursively traverse left subtree. Step 2 − Recursively traverse right subtree. Step 3 − Visit root node.